マイクロマウスの壁センサ
Tweetマイクロマウスでずっと使っている壁センサについて紹介します。
はじめに
いつかブログに書こうと思っていた、マイクロマウスの壁センサについて紹介します。 これは2016年に初めて作ったMIZUHOから使っているもので、ハーフサイズに出るようになった今でも部品やパラメータを変えつつ基本構成は同じまま使っている回路です。 もし同じようなことをやろうと思っている人がいたら参考になればと思います。
全体構成
全体構成はこのようになっています。 マイクロマウスの壁センサでよくある、赤外線LEDを壁に当てて反射してきた光の強度を測ることで壁との距離を測定します。
工夫したところの1つ目は、赤外線LEDを10kHzで点滅させ、受光回路+ソフトで反射光の10kHz成分だけを取り出している点です。 こうすることで自然光や点滅する照明などの外乱の影響を受けにくくすることができます。 赤外線LEDはマイコンからPWM信号を出すことで点滅させます(10kHz)。 受光した光はフォトダイオードで電流に変換し、 回路とソフトで自身が発光した10kHz成分の強度だけを抽出します。
2つ目は赤外線LED発光回路に定電流回路を使っていることです。 この回路によって部品のばらつきやバッテリー電圧の変動の影響を受けずに常に同じ電流をLEDに流すことができます。
回路とソフトの両方を組み合わせることで外乱に強くなる壁センサというわけです。
以降では赤外線発光回路、受光回路、ソフトウェアである周波数成分だけ取り出す方法について紹介していきます。
赤外線発光回路
回路
オペアンプとFETでこのような定電流回路を作っています。(2020/5/9 回路図中のCc, Rcを訂正しました)
オペアンプはVin = Vsとなるように出力電圧を制御をするため、結果的にLEDにはI = Vs / Rsの電流が流れます。 Rsが電流センス抵抗で、電流を電圧に変えてオペアンプに伝えているイメージです。 Vinに入れる信号はデジタルである必要はなく、アナログ的な信号を入れてLEDの電流を制御することもできます。
この回路で注意をすることは以下の2点です。
- オペアンプによるループが安定になり、欲しい反応速度が達成できるように部品を選ぶ
- LED, FET, Rsに適切な電圧がかかるように部品・入力電圧Vinを選ぶ
1については一巡伝達特性をみつつ安定かつ十分な応答が得られるように設計します。 この回路は、例えばダイオードと直列にL成分が入ると発振しやすくなるので、回路図上にはありませんが配線のL成分も考えて設計・シミュレーションをすべきです。 発振気味なときは回路図中のoptionalと書かれたCcとRcをいれると、Iの制御帯域がCc//Rcに制限される代わりにopamp回りの一巡伝達関数は安定な方向に変化します。 回路図中のFETを含む経路は負荷にLがつくと遅れ成分になるので、周波数の高い成分はCcを通して遅れなくopampに戻すとループはより安定になります。 Vsの変化の周波数の高い成分はフィードバックされないことになるので、Iの制御帯域は制限されていまします。
2はDCに関する設計です。 この回路ではFETはスイッチ動作ではなく飽和領域で動作させます。 なのでLEDに電流を流している時、RsやLEDで電圧降下が起きてもFETのdrain-source間に適切な電圧がかかるようにしないといけません。 そのためにバッテリー電圧、オペアンプに入力するVin(Rsにかかる電圧Vsでもある)をうまく調整します。
例えば3.3Vのマイコンのデジタル出力ピンを直接Vinに接続すると、VinとVsは0V↔3.3Vで動くことになります。 バッテリー電圧が3.7VだとFETとLEDで0.4Vしか使えないことになるのでうまく動きません。 その場合はVinには3.3Vを分圧し、Rsにかかる電圧を小さくすることで対応します。
マイコンによる制御
上の回路のVinにマイコンのPWMが出力できるピンを接続し、矩形波(duty 50%のPWM)を送っていました。 MIZUHOでは壁センサで測定をするときに10kHzの矩形波を4 pulse分入力していました。 使っていないときは0Vを入力しておけば無駄な電流を消費しません。
マイコンにDACが載っていればVinにアナログ的な電圧を入力し、LED電流を自由な波形に制御することもできそうです。
受光回路
回路
以下のような回路を使ってphotodiodeの電流を電圧に変換しています。 伝達特性は回路図に書いてある特性になります。
回路の基本部分はオペアンプで作るIV変換回路です。 オペアンプを使ったIV変換回路を使うと、マイコンのADCにはインピーダンスの低いオペアンプ出力を直接入力できるので無用なトラブルが減ります。
R1 C1でphotodiodeにバイアス電流を流しつつ、電流のDC成分はIV変換回路に流れないようにしています。 ここではHPFが構成されます。R1 C1でDC成分をカットし、後段ではAC成分だけを増幅しています。 DC成分をカットしておかないと、IV変換回路で環境光による直流成分が増幅されて出力電圧が飽和する可能性があります。 また、DCというより低い周波数を除去することである程度周波数を持った環境光の影響も低減させることができます。
photodiodeの電流のDC成分はカットしましたが、マイコンのADCは正の電圧しか扱えないのでVbiasだけoffsetさせています。 これによってVoutにはVbiasを中心に振動する信号が出力されます。 VbiasはマイコンのADCの基準電圧(電源電圧)の半分の電圧を抵抗分圧で作っていました。 オペアンプに入力するだけなので抵抗分圧で十分です。
電流 -> 電圧の変換時のDC gainはR2で決定します。 このgainは最終的に使用するphotodiode、赤外線LED、マイクロマウスの壁を使って実験的に決定しました。 gainが低いとノイズが増え、高いと飽和してしまうので丁度いい値にする必要があります。 LEDの光量や機体への取り付け方にも依存するので回路定数の決定は後回しにして、機体を組んでから調整したほうがいいかもしれないです。
R2と並列にC2を付けることで信号の高周波成分を落としています。 場合によってはオペアンプのループの安定性のためにR2 C2の値は制限を受けてしまうかもしれません。 欲しいDC gainと信号帯域だけではなく、そもそも回路を安定に動かすことも考慮してR2 C2は選ばないといけません。
この回路を最初に試しに作って見たときの定数ではI -> Voutの周波数特性は以下のようにしていました。 雰囲気band pass filterになっています。
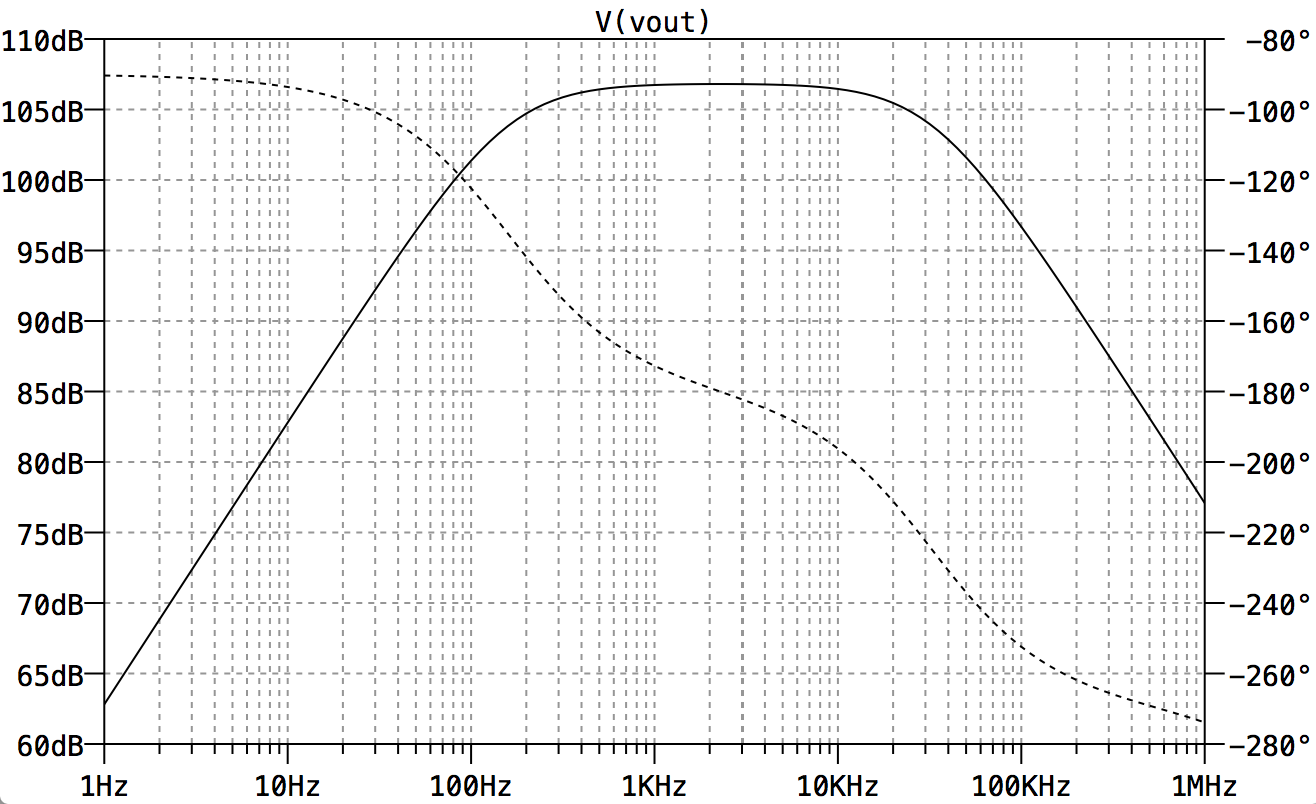
当初は2kHzくらいで赤外線LEDを点滅させることを考えていたので2kHzくらいがpass bandの中心になっています。 その後10kHzで点滅させることにしたので違った特性の回路を今は使っています。 どの周波数でカットするかはLEDの点滅周波数によって調整する必要があります。
こういうIV変換回路のDC特性はオペアンプのbias電流やoffset電圧の影響を大きく受けます。 今回はAD変換をした後にソフトでDCでないある周波数成分だけを取り出して使うので、DC errorはあっても問題ありません。 なのでオペアンプ回路の出力が飽和しない程度のものを選べば十分です。
マイコンによる制御
Vout端子はマイコンのAD変換ができるピンに接続し、ADCでアナログ値を読み取れるようにしました。 LEDを10kHzで点滅させていたので、それよりも十分に早い160kHzでサンプルをしていました。
マイコンはSTM32を使っていて、タイマーを使って160kspsでADCでサンプルし、 DMAを使ってメモリに結果を並べていました。 LEDは10kHzで4 pulse分出すと決めていたので、64 sample(DMAが64回転送)したらDMAから割り込みを発生させてデータの処理を開始していました。
ADCから得られたデータをplotすると以下のようになります。
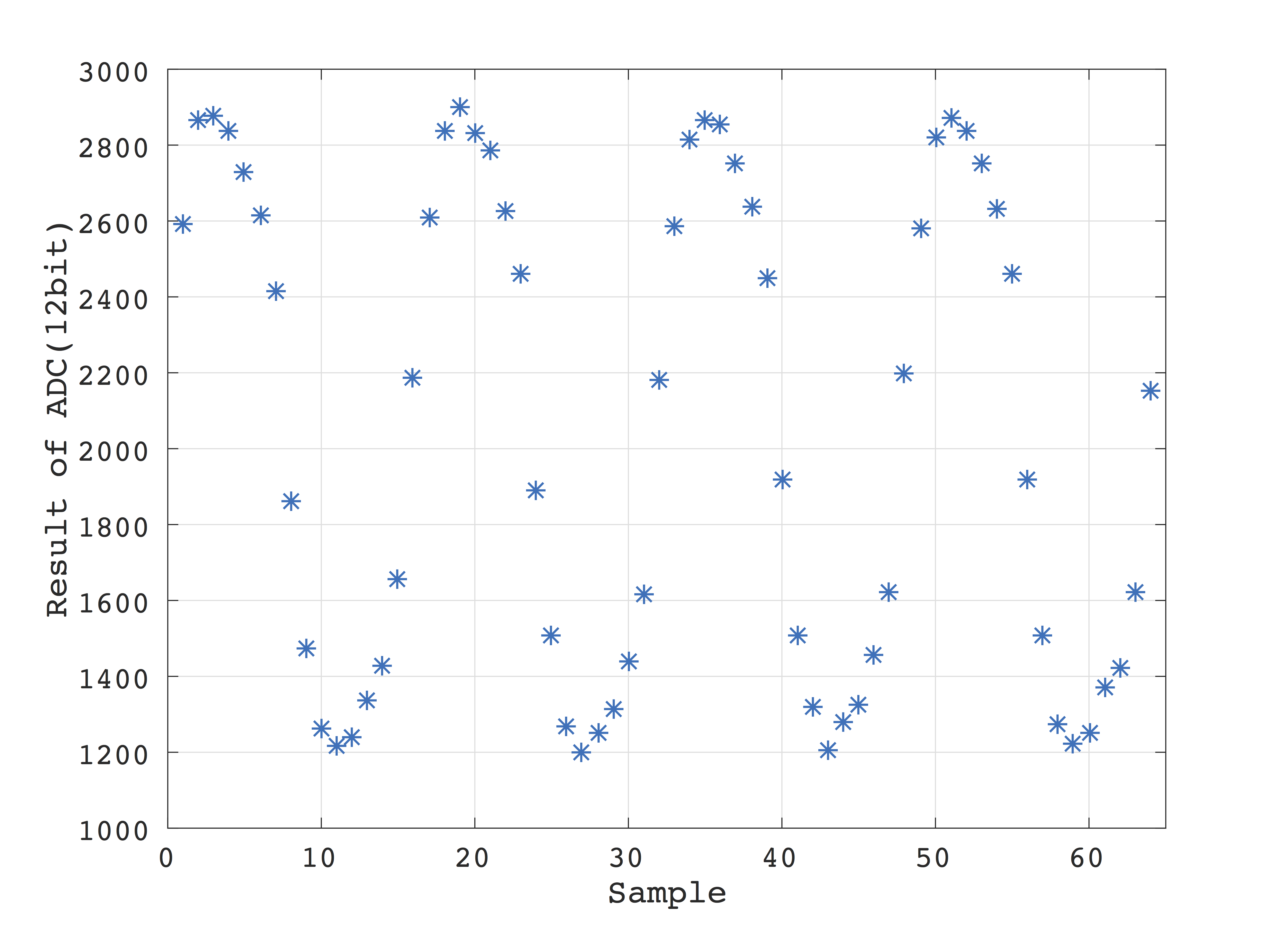
12bit ADCを使い、Vbias電圧をADC full scale電圧の半分に設定していたので、AD変換後のデータは2^12 / 2 = 2048を中心に振動しています。 10kHzの矩形波4 pulseを出力して測定したので、ちゃんと波が4周期あります。 また、回路のLPF特性によって高周波成分が消えているのがわかります。
以降ではソフトでこのデータから10kHz成分の強度を抽出していきます。
ソフトである周波数成分の大きさを計算する
受光した信号からある周波数成分の大きさを取り出します。 計算自体は離散フーリエ変換をある周波数についてのみ計算することと同じです。 抽出したい周波数のsin, cosとの内積を計算すればいいのです。 (この操作のことはなんと言えばいいのでしょうか?とりあえず直交復調と呼びます。)
受光した信号を\(x[k] (k=0,...,N-1)\)、サンプリング周波数を\(F_s\)とします。 ここでは\(x[n] (n=0,...,N-1)\)から周波数\(F_s \frac{n}{N}\\)成分の強度を計算します。
まず、ほしい周波数に相当する\(n\)に対して
\[X[n] = \sum_{k=0}^{N-1}x[k]\exp({-j\frac{2 \pi nk}{N}})\]を計算します。 次に複素数\(X[n]\)の絶対値を計算することで \(x[k]\)に含まれる周波数\(F_s \frac{n}{N}\)の振幅を得ることができます。
離散フーリエ変換ではすべての\(n=0,...,N-1\)について\(X[n]\)を計算しますが、 今は一つの\(n\)、つまり一つの周波数についての情報さえわかればいいので計算は簡単です。 上の計算式をそのまま計算してもいいのですが、exp()の部分の\(k\)についての周期性からある程度計算量を減らすことができます。
ちなみに先のADCで取得したデータをPC上で離散フーリエ変換すると以下のようになります。 \(n=4\)が10kHz成分なので、マイクロマウスの機体に実装したプログラムではこの\(n=4\)の部分だけの強度を計算しています。
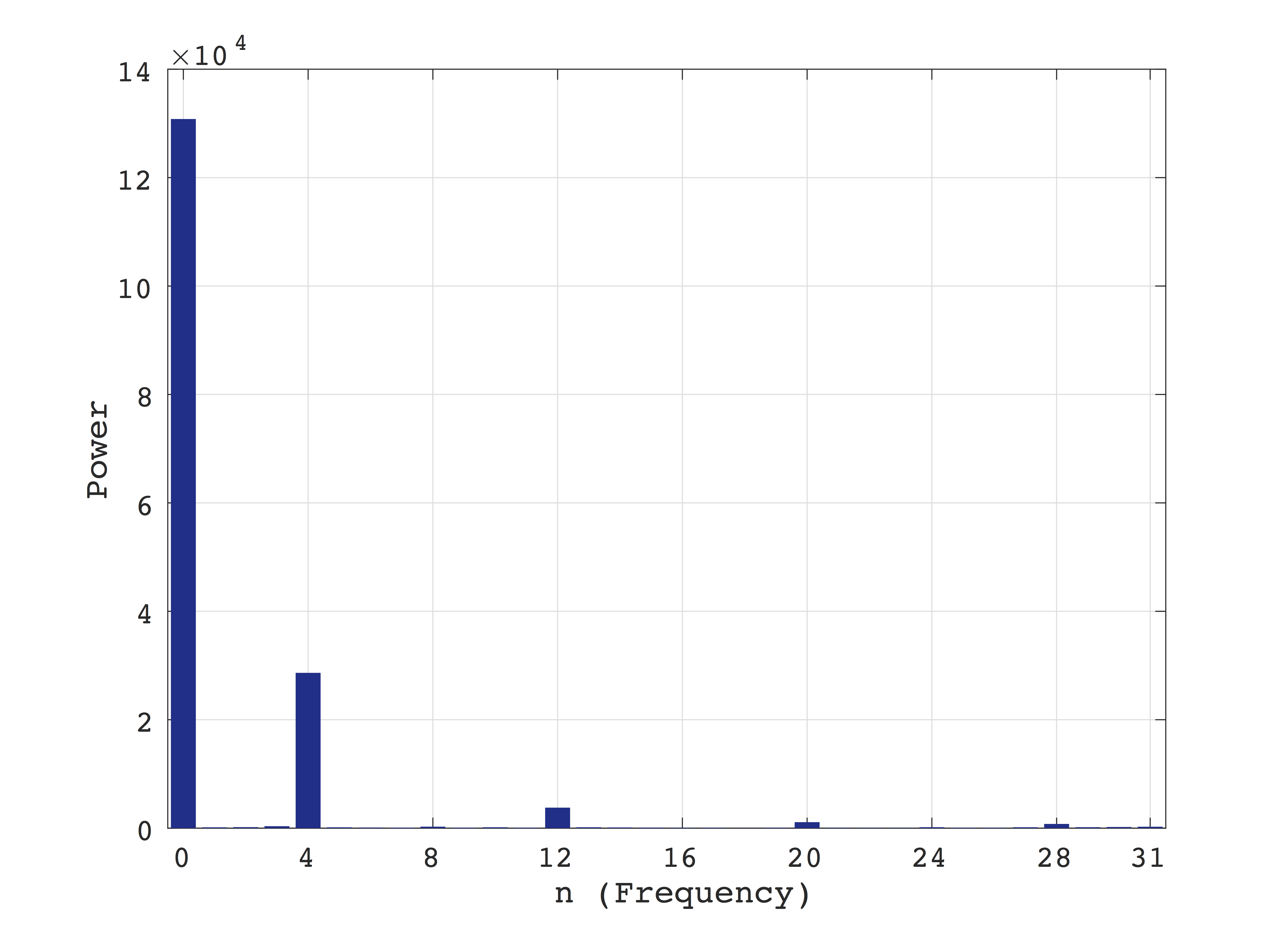
マウスに乗せて動かす
マウスの機体に回路とソフトを実装し、一定速度で走らせたときのセンサー値は以下のようになりました。 縦軸はADCで取得した生の値ではなく、ソフトで10kHz成分だけを抜き取ったものです。 どういう正規化をしていたのか忘れてしまいましたが、ADCの12bitに正規化されているわけではなさそうです。
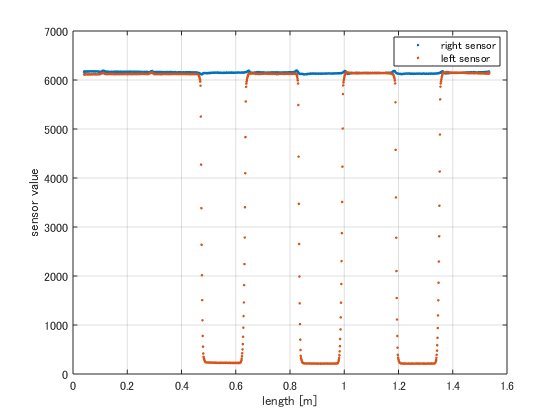
とりあえず、ロボットの走行中でも気になるノイズがなく壁センサーが使えていることがわかります。
おわりに
今回紹介した方法を一言でいうと、赤外線LEDとphotodiodeを使った壁センサを変調して使ったというわけです。 回路的にも外乱を受けにくくしていますが、ソフトでもLEDの点滅周波数成分だけを抽出しているところがポイントです。 一方で回路部品が多くなってしまうので。もう少し回路を小さくできるといいですね。
最適な構成か?といわれると怪しいですが、回路もソフトも新しいことに挑戦しつつそれなりに有用なものが作れた点は満足しています(2016年)。




