マイクロマウスの機体を同定する
Tweetシステム同定により、マイクロマウス機体(独立二輪駆動型の移動ロボット)の 左右のモーター電圧から車体の回転並進速度への伝達関数を出してみました。
はじめに
昨年度、ロ技研内にCheeseというマイクロマウスのチームが設立されました。 最近ではチーム内での交流も増え、私自身もマイクロマウスへの意識が高まっています。 現在は今年のマイクロマウスの大会に向けて、マイクロマウス機体MIZUHOv2の製作を進めています。

ハードウェアはとりあえず完成したので、次は制御部分の製作にとりかかっています。 マイクロマウスの制御系は下のようなものを考えています。
この制御系を設計するためには制御対象(図中の機体と書かれた部分)が数理的にモデリングできている必要があります。 今回の目的はこの制御対象をモデリングすること、端的にいうと伝達関数を求めることです。 制御対象のモデルが正確に分かっていると次のようなメリットがあります。
- 理論的に安定性・制御性能を評価できる
- PC上で機体の振る舞いをシミュレーションできる
- 制御パラメータを最適化できる
- センサのフィルタの設計(オブザーバ・カルマンフィルタなど)にも使える
制御対象を特にモデリングせずに実際の動きを見ながら制御パラメータを調整していく方法もありますが、 その方法で制御パラメータをいい感じに合わせられるのは上の図でいう速度コントローラくらいで、位置コントローラの調整までするのはなかなか大変です。 そんな時に制御対象のモデルがあれば、少なくともPC上でシミュレーションをして制御パラメータを試行錯誤的に決めることができます。 もう少し踏み込むと、実機もしくはシミュレーションで試行錯誤的に制御パラメータを調整することができても、その値は何も最適性を持っていない値になってしまいます。 制御理論の内には最適な制御パラメータを決める手法(例えば\(\mathcal{H}_\infty, \mathcal{H}_2\)ノルムに基く最適化) があるので、いずれそれらを使っていきたいです。そういったことをする場合にも制御対象のモデルが分かっている必要があります。 このように制御対象をモデリングする理由は色々挙げられますが、マシンが動いたらいいではなく、何が起こっているかを理解したいという個人的な思いが一番の理由だったりします。
動的システムをモデリングするためにはまず、運動方程式や回路方程式、幾何的な拘束などをもとに入出力関係を数学的に記述します。 入出力関係が記述できたらそれを伝達関数表現や状態空間表現といった形に変形し、制御問題を考えていきます。 今回は図中の機体と書かれた部分を入力が左右のモーターの電圧、出力が車体の回転速度と並進速度である2入力2出力の動的システムとして考えていきます。
システム同定とは
例えばシステムをモデリングするために運動方程式を立てる際に、質量が必要であれば実際の数値を用いるのではなく、とりあえず\(M\)という文字で置くことが多いでしょう。 こういった物理量を文字で置いた運動方程式から計算される伝達関数や状態空間モデルは、構造は定まっているが\(M\)などのパラメータに具体的な値が入っていない状態になっています。 最終的に制御系の設計をするとき(制御パラメータを決めるとき)には、この\(M\)に実際の値が入っている必要があります。 これらのパラメータは部品のデータシートからとってきたり、CADから算出したり、実際に測定する必要があります。 質量くらいなら簡単に精度よく測定することができるのですが、慣性モーメントや粘性摩擦を計測するのはなかなか難しいです。 ちなみに以前製作した玉乗りロボットを制御する際には、 運動方程式を立てた後に物理量を直接計測したりCADから算出することで制御対象をモデリングをしていました。
このように物理パラメータを測定して代入していく方法に対して、 ダイナミクスを知りたいシステムに適当な信号を実際に入力し、出力を計測することで中身を推定しようというのがシステム同定です。 システム同定といわれるものにもいろいろな種類があり、例えば 本当に何もわからない状態で入出力データから伝達関数を推定するもの、 伝達関数の次元くらいは分かっているので伝達関数の係数を推定するもの、 伝達関数を構成する細かいパラメータ(運動方程式における質量\(M\)など)を同定するものなどがあります。 今回はまず運動方程式などから伝達関数を計算し、 同定実験からその伝達関数の係数はこうだろうという推定をしていきます。
参考文献
システム同定の基礎的なことについてはこの本に分かりやすくまとまっています。
システム論の基礎から同定手法の原理までMATLABのサンプル付きで紹介されています。 私自身もシステム同定は何も知らない状態からこの本を読んで、実際に試してみてこの記事を書いています。
話の流れ
この記事の以下の話の流れは次のようになっています。
- 伝達関数を計算する
- 実機のステップ応答を測ることでシステムの大枠をつかむ(プリ同定)
- いい感じの同定入力を決める
- 同定実験を行う
- 同定実験の結果からシステムを同定する
- 同定されたシステムの妥当性を検討する
これは実際に私が行った工程でもあり、おそらくシステム同定をするときの一般的な流れでもあると思います。
モデルの導出
マイクロマウスの左右のモーター電圧から車体の並進回転速度のダイナミクスを考えるために、 以下の図のような単純なモデルを考えます。 左の図は左右の各モーター\(i (i=1,2)\)の等価な回路モデルを、 右の図は車体の力学的なモデルを表しています。 より詳細なモデルとしてタイヤの変形や車体の傾き(ロールピッチ)も考慮したものもあるらしいのですが、 どうせ非線形になって制御問題を私は扱えなくなるので、今回は単純なモデルで考えます。 さらに問題を簡単にするために、モーターの特性は左右で等しく、車体の重心の位置左右のタイヤの軸上の中央にあるとしています。
左図中の \(u_i\)はモーターの両端電圧、 \(j_i\)はモーターに流れる電流、 \(\omega_i\)はモーターの回転速度、 \(\tau_i\)はモーターの出力軸のトルク、 \(\tilde{\omega}_i\)はタイヤの回転速度、 \(\tilde{\tau}_i\)はタイヤのトルク、 \(R\)はモーターの抵抗、\(L\)はモーターのインダクタンス、 \(K_e\)はモーターの逆起電力定数、 \(K_m\)はモーターのトルク定数、 \(B\)はモーターの出力軸からみた全ての粘性摩擦(減速後の部分も換算して含む)、 \(J\)はモーターの出力軸からみた全ての慣性モーメント(減速後の部分も換算して含む) です。 右図中の \(V\)は車体の並進速度、 \(\Omega\)は車体の回転速度、 \(M\)は車体の質量、 \(I\)は車体の慣性モーメント、 \(r_w\)はタイヤの半径、 \(r_d\)は車体の重心とタイヤの距離 を表しています。
まず、左図から式(1)を導くことができます。 式(1)の上の式は回路の電圧に関して成り立つ式です。モーターの起電力は\(K_e \omega_i\)になることに注意してください。 式(1)の下の式はモーターによって発生するトルクに関する釣り合いの式です。 モーターに流れる電流とモーターによって発生するトルクは比例関係にあり、 その比例定数を\(K_m\)とおいているので、等号の左側はモーターによって発生するトルクを意味しています。
\[\begin{align} \left\{ \begin{array}{l} u_i &=& R j_i + L \frac{dj_i}{dt} + K_e \omega_i \\ K_m j_i &=& B \omega_i + J \frac{d\omega_i}{dt} + \tau_i \end{array} \right. \end{align}\]今回はモーターの出力軸とタイヤとの間にギア(減速比\(N\))をかませているので、 モーターの出力軸とタイヤの間のトルクと角速度について、式(2)が成り立ちます。
\[\begin{align} \left\{ \begin{array}{l} \tilde{\omega}_i &=& \frac{1}{N} \omega_i \\ \tilde{\tau}_i &=& N \tau_i \end{array} \right. \end{align}\]車体は2次元平面上で回転運動と並進運動をするとしているので、 並進と回転についての運動方程式から式(3)が成り立ちます。
\[\begin{align} \left\{ \begin{array}{l} M \frac{dV}{dt} &=& r_w ( \tilde{\tau}_1 + \tilde{\tau}_2) \\ I \frac{d\Omega}{dt} &=& \frac{r_w}{r_d}( -\tilde{\tau}_1 + \tilde{\tau}_2) \end{array} \right. \end{align}\]また、タイヤの回転速度、車体の回転速度、車体の並進速度は幾何的な関係から式(4)が成り立ちます。
\[\begin{align} \left\{ \begin{array}{l} V &=& \frac{r_w}{2}(\tilde{\omega}_1 + \tilde{\omega}_2) \\ \Omega &=& \frac{r_w}{2r_d}(-\tilde{\omega}_1 + \tilde{\omega}_2) \end{array} \right. \end{align}\]次に、これらの式(1)~(4)を制御を考えるときに扱いやすい形に変形していきます。
伝達関数モデル
動的システムをモデリングするために、まずは入出力を何にするかを定義します。 今回は入力\(u\)、出力\(y\)を次のように取ります。
\[u = \begin{bmatrix} u_1 \\ u_2 \end{bmatrix}, \ y = \begin{bmatrix} V \\ \Omega \end{bmatrix}\]式(1)~(4)を見た感じ\(u,y\)の関係は線形微分方程式で記述できるので、今回扱うシステムは線形システムであることが分かります。 線形システムの表記方法の一つとして、 \(u \to y\)の伝達関数行列(\(u, y\)がベクトルなので行列)を求めてみます。 式(1)~(4)をラプラス変換し、\(y(s) = {\bf G}(s) u(s)\)となる\({\bf G}(s)\)を計算をすると次のようになります。
\[\begin{align} {\bf G}(s) = \begin{bmatrix} G_V(s) & G_V(s) \\ -G_\Omega(s) & G_\Omega(s) \end{bmatrix} \end{align}\]ただし\(G_V(s), G_\Omega(s)\)は以下の通りです。
\[G_V (s) = \frac{b_{v0}}{a_{V2}s^2 + a_{V1} s + a_{V0}} \\ a_{V0} = 2N^2(K_mK_e + BR), \ a_{V1} = MR + 2N^2(BL + JR), \\ a_{V2} = ML+2N^2JL, \ b_{V0} = K_m N r_w\] \[G_\Omega (s) = \frac{b_{\Omega0}}{a_{\Omega2}s^2 + a_{\Omega1}s + a_{\Omega0}} \\ a_{\Omega0} = 2N^2r_d(K_mK_e + BR), \ a_{\Omega1} = r_d(IR + 2N^2(BL + JR)), \\ a_{\Omega2} = r_d(IL+2N^2JL), \ b_{\Omega0} = K_m N r_w\]ここで求めた伝達関数行列\({\bf G}(s)\)の特徴として、次のようなことが挙げられます。
性質1 分母多項式は2次式で、分子多項式は0次式
各伝達関数の分母多項式が2次式ということは2つの極をもち、分母多項式が0次式ということは零点は持たないということが分かります。 ついでに分母多項式が2次式で、係数はすべて正なので安定な伝達関数であることも分かります。 これらの情報は同定をする時と、同定結果の妥当性を検証する時に大きなヒントになります。
性質2 \({\bf G}(s)\)は2つの伝達関数で記述することができる
\({\bf G}(s)\)は2入力2出力の伝達関数行列なので一般的には4つの伝達関数を行列の成分に持ちます。 しかし今回はその4つの伝達関数が2つの伝達関数\(G_V(s), G_\Omega(s)\)で表現することができます。 これは機体をモデリングするときに左右のモーターの特性が等しかったり、 機体の重心が車軸上の中央にあるという仮定を置いたから成り立つ性質です。 ここではこの特徴についてもう少し考えてみます。
次のような行列\(T\)
\[T = \begin{bmatrix} 1 & 1 \\ -1 & 1 \end{bmatrix}\]を使って入力\(u\)を新たな入力\(\hat{u}\)
\[\hat{u} = \begin{bmatrix} \hat{u}_1 \\ \hat{u}_2 \end{bmatrix} = T u = \begin{bmatrix} u_1 + u_2 \\ -u_1 + u_2 \end{bmatrix}\]に変換してみます。 このとき\(\hat{u} \to y\)の伝達関数行列\(\hat{\bf G}(s)\)は
\[\hat{\bf G}(s) = {\bf G}(s) T^{-1} = \begin{bmatrix} G_v(s) & 0 \\ 0 & G_\Omega(s) \end{bmatrix}\]となります。\(\hat{\bf G}(s)\)が対角行列になっているのがポイントです。 \(\hat{\bf G}(s)\)が対角行列であるということは、 \(V\)は\(\hat{u}_1 = u_1 + u_2\)の影響のみを受け、 \(\Omega\)は\(\hat{u}_2 = -u_1 + u_2\)の影響のみを受けるということです。 考えているシステムは2入力2出力のMIMOなシステムでしたが、いい感じの入力変換をすると2つの独立なSISOなシステムとして考えることもできるということです。 一般的にMIMOなシステムは複数の入力が混ざって複数の出力に出ていくのでなかなか考えるのが難しいです。 それが簡単なSISOなシステムに分解できたのは非常にうれしいことです。 この性質は以降もどんどん使っていきます。
少し話はそれますが、マイクロマウスをはじめとする独立二輪駆動型の移動ロボットを制御する際に
- 左右のモーター電圧の和\(u_1 + u_2\)で車体の並進速度\(V\)を制御
- 左右のモーター電圧の差\(-u_1 + u_2\)で車体の回転速度\(\Omega\)を制御
という制御手法を聞いたことがありませんか? この手法は先ほど導かれた
- 車体の並進速度\(V\)は左右のモーター電圧の和\(u_1 + u_2\)の影響のみを受ける
- 車体の回転速度\(\Omega\)は左右のモーター電圧の差\(-u_1 + u_2\)の影響のみを受ける
という事実に基づいているのだと思います。 直感でなんとなく妥当な気もするのですが、ダイナミクスを記述することで妥当性をちゃんと確認することができます。
ステップ応答を得る
同定実験をする前に、ステップ応答を見てダイナミクスの大まかな性質(定常ゲイン、立ち上がりの速さ)を調べてみます。 この情報は同定実験をするための同定入力を決定するときや、同定結果の妥当性を検証するときに使います。 ちなみにシステム同定の基礎 では、このような同定の前に行う簡単な計測をプリ同定と呼んでいます。
まずは回転方向について実験をしてみました。 マウスの左右のモーターに同じ大きさで逆向きの電圧を掛けて、その時の車体の回転速度のログを取ります。 MIZUHOv2にはSDcardを読み書きする機能があるので、左右のモーターに取り付けられたロータリーエンコーダやジャイロセンサの値をSDcardに記録しておき、 PC上で車体の並進回転速度を算出しています。
この実験をしているときの動画はこんな感じです。 ただ回転するだけです。
この実験によって得られた\(G_\Omega(s)\)のステップ応答に相当する回転速度の応答は以下の通りです。
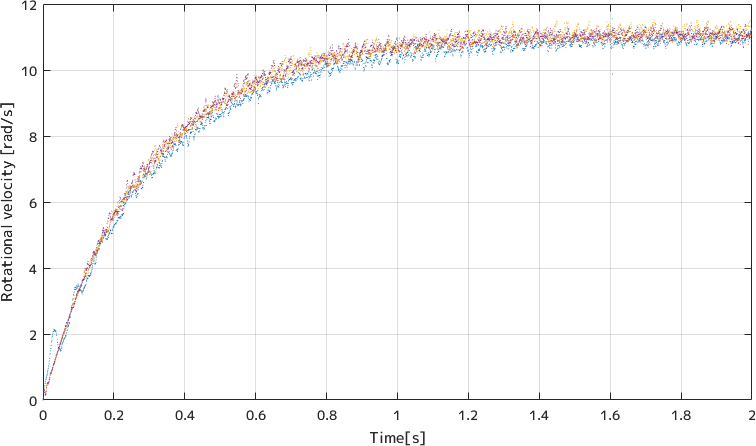
これは回転速度の生データではなく、左右のモーターに掛けた電圧の差が1[V]になるように正規化したものになっています。 なので大きさ1のステップ入力を\(G_\Omega(s)\)に入力したときの応答に相当します。
続いて並進速度に関する伝達関数\(G_V(s)\)のステップ応答に相当する並進速度の応答は次のようになります。
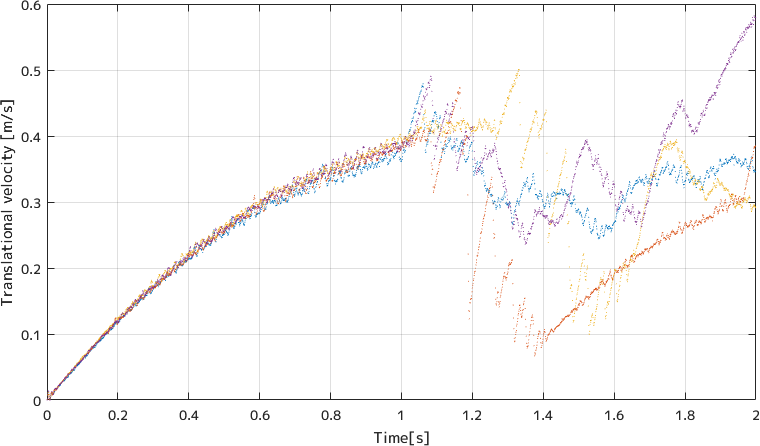
これは左右のモーターに掛けた電圧の和が1[V]になるように正規化しています。
モデリングをする際に左右のモーターの特性が等しかったり、重心が車軸上の中央にあるという仮定を置いていました。 もしその仮定が完全に正しいものであれば左右のモーターに等しい電圧を掛ければ機体は真っすぐ走るはずです。 しかし現実には左右で違いが出てしまうので真っすぐは走ってくれず、緩やかに曲がっていきます。 実験のために広い場所を確保することができなかったので、すぐに周りのものにぶつかってしまい1秒間のデータしかとることができませんでした。 できれば応答が整定するまでのデータを取りたかったのですが、あきらめました。
次に、このステップ応答から得られる情報から同定入力を決めていきます。
同定入力を決定する
今回システム同定をしてみて分かったのは、同定入力を決定するのが一番難しいということです。 入出力データからシステムを推定する部分は数多くの手法が提案されていて、 それらはMATLABに実装されています。 なので私たちシステム同定したいユーザー視点では、同定入力をいかに決めるかが唯一設計しないといけない部分であり、同定精度の全てがかかっています。 同定する対象の特性を見極めて、いい感じに決める技術が必要とされています。
私自身、いまだに最適な同定入力の決め方はよくわかっていませんが、ある程度の指針やトレードオフはつかめたような気がするので、 システム同定の基礎 に書いてあった知見と実体験をもとに感じたことを書いていきます。
M系列信号
同定実験によって伝達関数を同定するということは、周波数応答(ボード線図)を知ること考えることができます。 なので、例えば1Hzから1Hz刻みで100Hzまでの正弦波を用意して、 それぞれの正弦波を入力した時に出力される正弦波の振幅と位相情報を集めれば周波数応答を知ることができます (線形システムに正弦波を入力すると、入力された正弦波と同じ周波数で位相と振幅が変化した正弦波が出力される)。 この方法はこの場合では100回実験を行う必要があり、非常に大変です。
そこで単一の周波数成分をもつ正弦波を入力するのではなく、それらの正弦波を足し合わせたものを入力して 複数の周波数を同時に測定しよう考えします。 複数の周波数成分を持つ入力は、理想的にはすべての周波数成分を持つ入力でです。 このような理想的な入力は、例えばホワイトノイズ(無限長)です。 実際には理想的なホワイトノイズを使った実験は不可能なので、ある程度妥協をします。 妥協した結果よく使われる入力がM系列信号です。
M系列信号の性質はググるとたくさん出てきますが、 システム同定においては
- 有限長の信号である
- 実際に実験することが可能)
- ホワイトノイズに近い統計的性質を持つ
- ランダム性
- 非常に多くの周波数成分をまあまあ均等に含む
- 2値の信号で扱いやすい
- 線形システムは2値信号で同定することが可能
といった性質があるためによく使われます。
同定対象の性質によってはM系列信号以外の入力信号の方が適している場合もあります。 今回に限っては、とりあえず最も標準的なもので試してみたい理由から入力信号はM系列信号で考えていきます。
じゃあどんなM系列信号がいいのかという話になるのですが、 まずは決めないといけないM系列信号のパラメータを挙げておきます。
- 振幅
- シフトレジスタの長さ
- クロック周期
ここからはこの3つのパラメータをどのようにして決定していくかについて考えていきます。
M系列信号の振幅
入力信号の振幅が小さいと 摩擦や不感帯などの非線形要素の影響が無視できなくなったり、センサの分解能やSN比的に出力信号の計測精度が落ちるor計測できないといったことが起こります。 マイクロマウスにおいてはモーターの電圧をとても小さい振幅で振動させた場合、 モーターの出す力よりも摩擦の方が大きいため、きっと機体は動きません。(摩擦のない理想的な線形モデルであれば機体も小さく振動するはずなのですが)
入力の振幅を大きくしていくと先に挙げた問題は起こらなくなります。 しかし入力が大きすぎると今度はアクチュエータの飽和が起こったり、 マイクロマウスの場合だとタイヤのスリップが起こってしまいます。 これまた非線形要素が無視できなくなるということです。 加えて、マイクロマウスの場合だと大きい入力を入れるとその分マウスが長い距離移動することになるので、 同定実験のためにより広い場所が必要となり、困ります。
結論として、小さすぎず大きすぎずの振幅をうまく選んでやる必要があります。 同定対象の特性をよく考えながらいい感じに決めます。
M系列信号のシフトレジスタの長さ(n)
シフトレジスタの長さはM系列信号の周波数スペクトルの平坦さ、実験の長さ(時間)、この後に出てくるクロック周期に関係します。 クロック周期との兼ね合いは後で説明するので、それ以外の要素について考えます。
M系列信号は長さを無限に取ってやると(それはM系列信号なのか?)、全ての周波数成分を均等な大きさで持ちます。 なのでシフトレジスタの長さが長いほど、M系列信号の周波数成分はどの周波数でも均一になり、きっと同定精度も上がっていきます。 ただ、実際にはほかの要因で同定精度が落ちるため、ある程度の長さがあれば十分です。 別の問題として、シフトレジスタの長さを長くするほど純粋に入力信号1周期分の長さは長くなるため、同定実験に非常に時間がかかるようになります。 マイクロマウスの場合だと、M系列信号の振幅を大きくした時と同様に実験をするために広い場所が必要になってしまうので、 あまり長くても困ります。
これも色々試していい感じに決めます。
M系列信号のクロック周期(Tc)
これは適当にやったらまったく同定ができなかった要素なので少し詳しく書いておきます。
M系列信号はシフトレジスタによって生成され、そのシフトレジスタをどれくらいの周期でシフトしていくかというパラメータがあります。 それをM系列信号のクロック周期と呼びます。 このクロック周期はM系列信号のうち、1が持続する最も短い時間でもあります。
M系列信号は理想的には全ての周波数成分を含んでいてほしいのですが、実際にはクロック周期Tcと先に紹介したシフトレジスタの長さnによって信号の周波数成分が制限されます。
M系列信号は矩形波の集まりと考えれば高周波成分はたくさん含んでいるのですが、低周波の方はそうでもありません。 クロック周期がTcでシフトレジスタの長さがnのM系列信号は1が持続する最も長い時間はnTcになるので、 このパルスよりも周波数成分が低い情報は精度よく同定することはできません。
これによって問題が起こるのは定常ゲイン(低周波域)の同定精度です。 システム同定の基礎 によると定常ゲインを精度よく同定するには、 M系列信号の1が持続する最も長い時間nTcは、同定対象の立ち上がり時間よりも長い必要があるらしいです。 つまり、出力が十分に飽和するくらい長く入力が持続する必要があるということです。 最初にプリ同定としてステップ応答を計測してあれば立ち上がり時間を知ることができるので、 その情報をもとにクロック周期Tcやシフトレジスタの長さnを決めていきます。
ここでの話は、同定入力であるM系列信号のクロック周期(Tc)を変化させると出力はどのように変化するかを見るとよく分かったので、 簡単なシミュレーションを紹介します。 ここでは伝達関数\(G(s) = \frac{1}{s + 1}\) に振幅1、シフトレジスタの長さ7のM系列信号を入力して違いを見てみます。
クロックの周期が短すぎる場合(周期0.1[s])はこんな感じの応答になります。
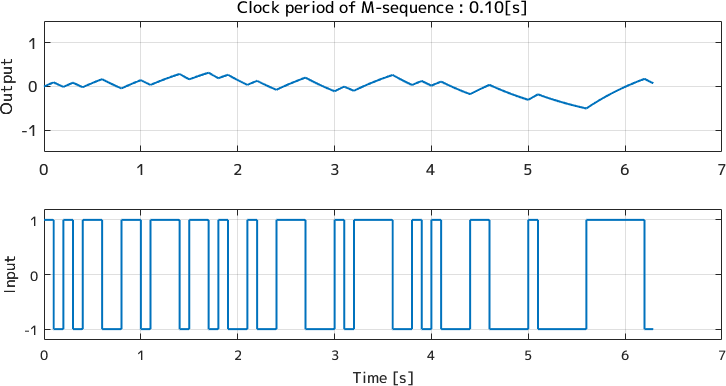
伝達関数\({\bf G(s)}\)のゲインは1なので出力は±1で変化をするはずですが、 入力の変化が速すぎて出力は全く振れません。 出力が飽和していないので、これだと定常ゲインを含む低周波域が全く同定されません。
逆にクロックの周期が長すぎる場合(周期10[s])はこんな感じの応答になります。
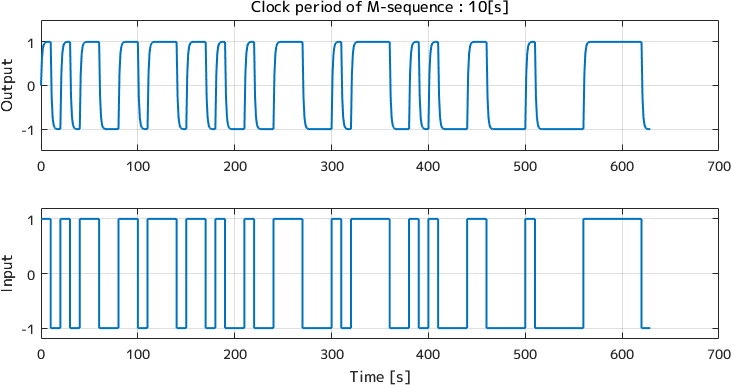
得られた信号のほとんどは定常値に落ち着いた状態になっていて、過渡的な成分の比率は信号全体に対して非常に小さくなっています。 定常ゲインは精度よく求められるかもしれませんが、過渡的な応答は全く同定されないでしょう。
最後に同定したいモデルの本質的な部分がよく表れるように適切にクロックの周期を決めてやった場合についてです。 ここではクロックの周期を1[s]にしています。
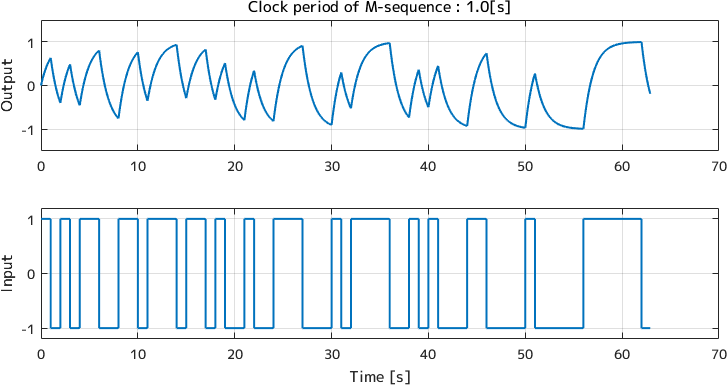
グラフを見て分かる通り、±1の範囲でよく振れていて、過渡的な信号がたくさん得られているのでおそらく\(G(s)\)のゲイン線図が折れるあたりが精度良く同定できます。 また、時刻35秒や60秒あたりでしっかりと飽和しているので、定常ゲインも精度よく同定されるはずです。
決定した同定入力
同定したいシステムはMIMOですが、先に紹介した入力変換によって二つのSISOなシステムに分解することができました。 今回はMIMOなシステムを直接同定するのではなく、2回の同定実験を行うことで二つのSISOなシステムを同定します。
その2つの同定実験のための入力は、色々試した結果次のようなものを用いることにしました。
| シフトレジスタの長さn | 入力の長さN | シフトレジスタのクロック周期Tc[s] | M系列信号の振幅[V] | センサのサンプリング周期Ts[s] | |
|---|---|---|---|---|---|
| 並進方向 | 6 | 63 | 0.4 | 2.5 | 0.02 |
| 回転方向 | 7 | 127 | 0.2 | 2.5 | 0.02 |
すでにステップ応答を実験的に得ているので、立ち上がり時間を計算することができます。 その立ち上がり時間の情報を利用して、出力が十分に飽和するようにシフトレジスタの長さnやシフトレジスタのクロック周期Tcを決定しています。
並進方向の同定に使うM系列信号のシフトレジスタの長さはもっと長くしたいのですが、 実験できる場所の広さの関係でこの値にとどめています。
センサのサンプリング周期は十分短い周期である0.02[s]にしています。 システム同定の基礎 によると、同定をするときに最適なサンプリング周期があるらしいのですが、 とりあえずセンサのサンプリング周期はデータを取る段階では十分に早く取っておけば、 後からDecimationフィルタを通してデータを間引けばサンプリング周期を落とすことは可能です。 ただ、今回は0.02[s]でデータを取った後にダウンサンプリングして同定すると同定精度が落ちてしまったので、 0.02[s]でサンプルしたデータを直接使って同定しています。
同定実験
先ほどのM系列信号を使って、並進方向と回転方向の2つに分けて同定実験を行います。
同定をするときに実験で得られたデータを同定用と検証用の二つに分割をしてCross Validationを行うので、 M系列信号2周期分の実験を行います (M系列信号の特性はあくまでM系列信号1周期分すべてのデータを利用できた場合の話なので、同定用に1周期分を確保する必要がある)。 まったく同じM系列信号を繰り返してCross Validationをしても意味がないので、 元のM系列信号にそれを半周期分ずらしたものを付け足して入力としています。
まず、並進方向の実験をしてみました。 M系列信号を左右のモーターに同相で入力します。 その時の動画はこちらになります。
体育館の一角を借りて実験をしたのですが、床のほこりやテープが原因でよくスリップしています。 並進のステップ応答をとった時と同様に、直進する制御などは入れていないので、どうしてもカーブしながら走ってしまいます。 結果的には多少カーブしてしまってもまあまあ同定できます。この時の入出力をプロットしたものがこちらになります。
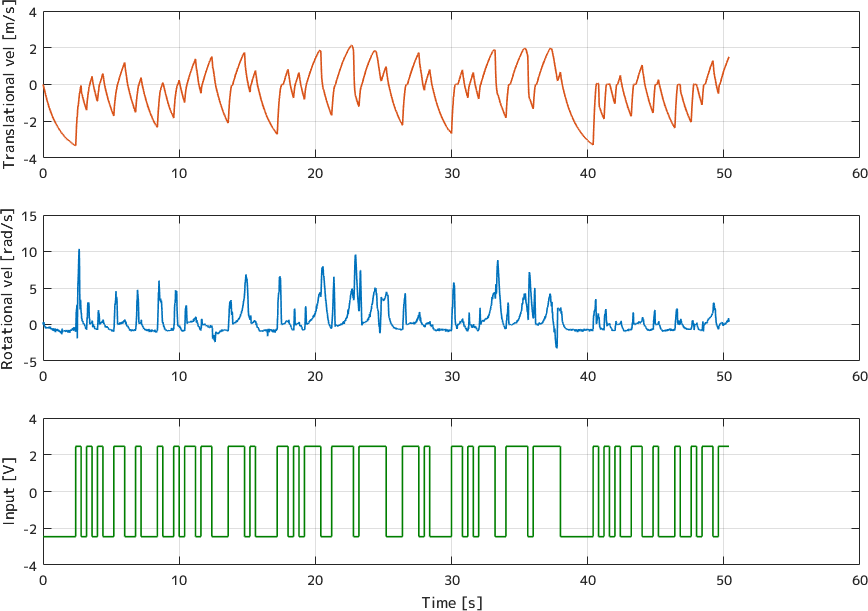
上から順に並進速度、回転速度、入力の大きさ(左右で同相)になります。 並進速度がよく振れているのは当たり前ですが、 回転速度も結構振れてしまっています。 回転速度はだいたい正の値を持っているので、車体は反時計回りに回転をし続けていたということになります。 これは車体が完全に左右対称ではないからだと考えられます。
続いて回転方向の実験をしました。 M系列信号を左右のモーターに逆相(符号をお互いに逆にして)入力します。 その時の動画はこちらになります。
回転方向はあまり動き回らないので楽です。 この時の入出力をプロットしたものがこちらになります。
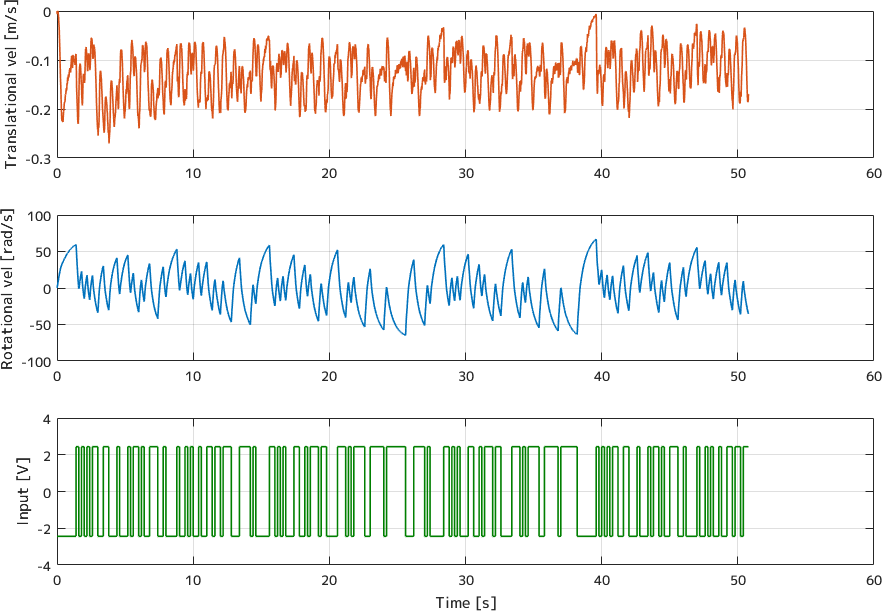
上から順に並進速度、回転速度、入力の大きさ(左右で逆相)になります。 並進速度はほとんど振れていないので、いい感じです。
次はこれらのデータとMATLABを使って実際に同定をします。
MATLABでモデルを同定する
MATLABのSystem Identification Toolboxを使います。 System Identification Toolboxには様々な同定アルゴリズムがすでに実装されていて、パッと使うことができます。 GUIも用意されているのでポチポチしてるだけでデータの前処理->同定->評価を簡単に行うことができます。 色々試してどう同定するのが適しているかを探る場合にはとても有用です。
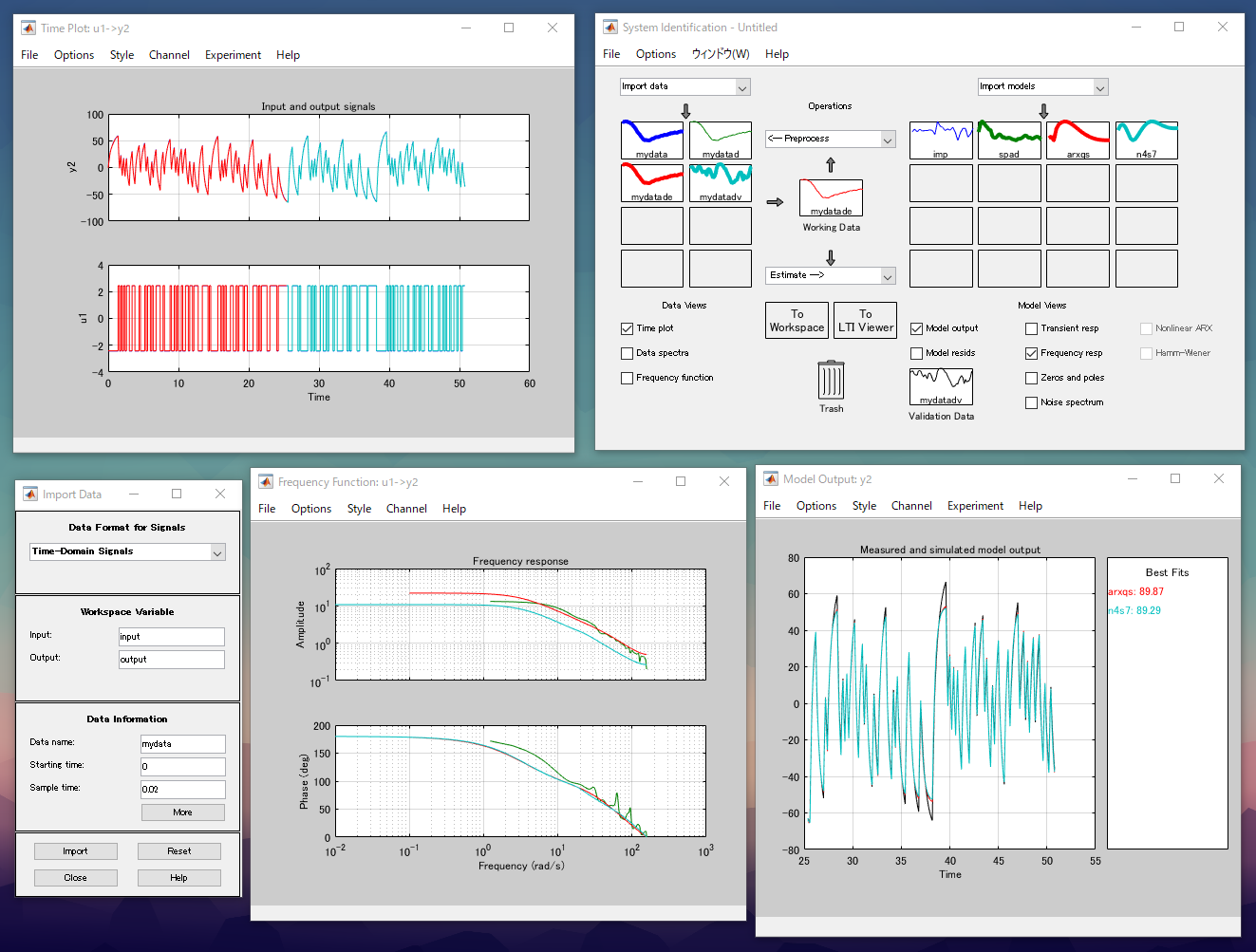
これらのツールの使い方は公式のマニュアルやチュートリアルが充実しているので、解説はそちらに任せます。
同定結果
今回は先の紹介をしたGUIを使って以下の作業を行いました。
- データを読み込む
- 外れ値、バイアス(トレンド)を除去する
- データを前半と後半の2つに分割する
- 前半のデータを用いて、N4SID法で伝達関数(極2個、零点0個で拘束)を同定する
- 同定された伝達関数を後半のデータを使って検証する
この作業の結果、回転方向の伝達関数はこのように同定されました。
\[G_\Omega(s) = \frac{3.654e04}{s^2 + 952.5 s + 3324}\]その時のMATLABのログは次の通りです。
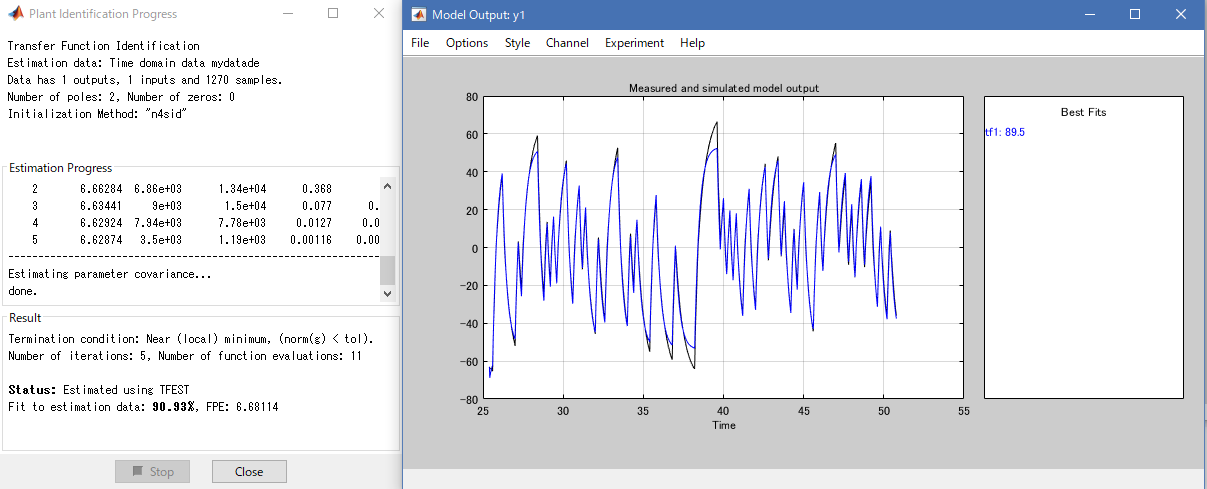
いい感じです。
並進方向の伝達関数はこのように同定されました。
\[G_V(s) = \frac{1.66e04}{s^2 + 1.844e04 s + 3.945e04}\]その時のMATLABのログは次の通りです。
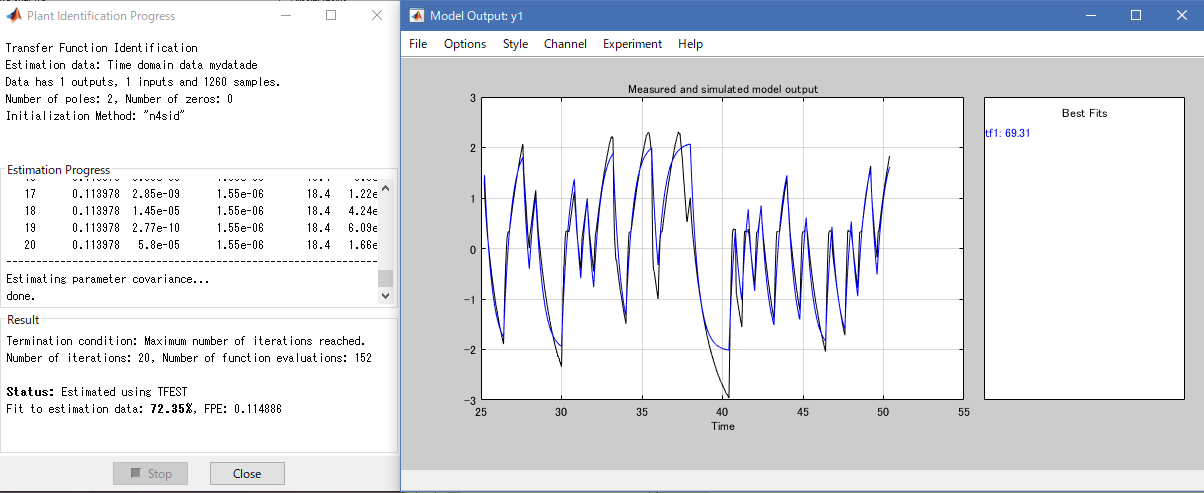
回転方向の時と比べてフィット率は低くなっています。
同定実験の結果を見てもわかる通り、 機体が完全に左右対称ではないので回転方向にも結構動いてしまったり、タイヤが空回りしてしまっているのがズレの原因と考えられます。 純粋に精度よく同定できていない可能性もありますが、 ちゃんと同定はできてはいるが、タイヤの空転によりそもそもデータが正しくないのでフィット率が下がってしまっている可能性もあります。
ステップ応答の比較
最初にステップ入力を入れたときの応答がとってあるので、それと同定によって得られた伝達関数のステップ応答を比較してみます。
回転方向はこうなりました。
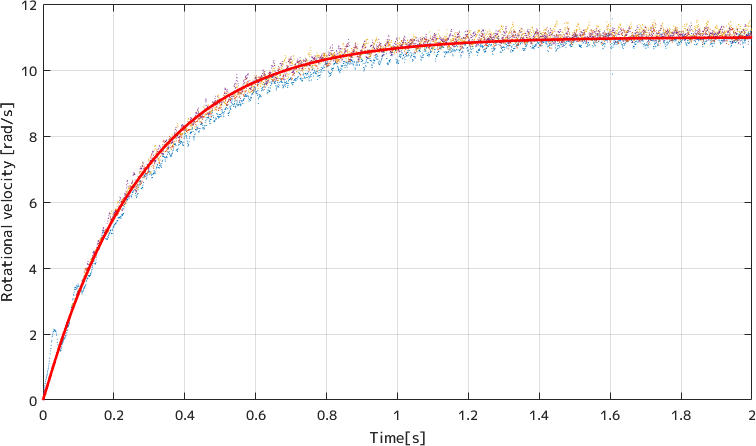
図中の赤い線が同定された伝達関数のステップ応答です。 完全に一致ですね。
並進方向はこうなりました。
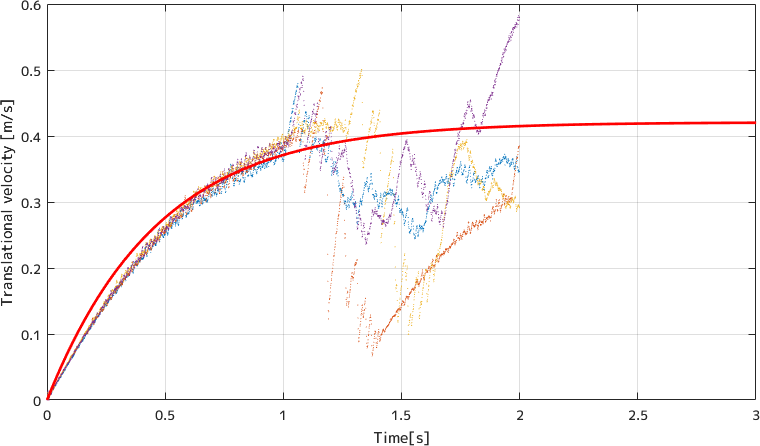
若干ずれているので心配なところですが、 のちにコントローラを設計するときにはそれほど問題にはなりませんでした(そのうち記事を書きます)。
まとめ
マイクロマウス機体の 左右のモーターの電圧から車体の並進回転速度までの伝達関数を同定することができました。
入出力データから伝達関数を同定する部分はMATLABがやってくれるので、 私たちがやらないといけないのは同定入力を決定し、実験をすることです。 実際に同定をしてみて、同定入力を作る部分が重要だと分かったので、 いかに同定入力を作るかについては今後も勉強をしていきたいと思います。
この話の続きとして、今回同定したモデルを使って制御系を設計していく話もあるので、 そちらは後日記事を書きます。



